部材内部に生じる応力には①「軸方向力(軸力)」、②「せん断力」、③「曲げモーメント」の3つがあります.
|
応力
|
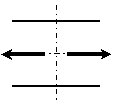 引張力(+) 引張力(+)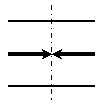 圧縮力(-) 圧縮力(-) |
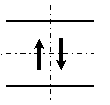 (+) (+)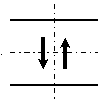 (-) (-) |
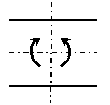 (+) (+)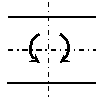 (-) (-) |
|
軸方向力
|
せん断力
|
曲げモーメント
|
|
|
記号
|
N
|
Q
|
M
|
軸力では引張力を(+)、圧縮力を(-)、 せん断力では、時計回りの力の向きを(+)、反時計回りの力の向きを(-)、 曲げモーメントでは、下側に引張力を生じさせる対のモーメントを(+)、下側に圧縮力を生じさせる対のモーメントを(-)としています.
応力図を描く場合、応力の符号というものが重要になってきます.応力図に符号をつけることで,部材中にどのような状態の応力がいくらの大きさで生じているか分かるようにするためです.応力図とその符号を下に示します.
|
応力図 |
 |
 集中荷重の場合 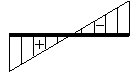 等分布荷重の場合 |
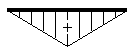 集中荷重の場合 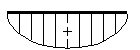 等分布荷重の場合 |
|
図名
|
軸方向力図 (N図)
|
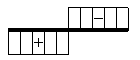
せん断力図 (Q図)
|
曲げモーメント図 (M図)
|
軸力については符号と応力図の向き以外に注意する事はありませんが,せん断力図と曲げモーメント図については、集中荷重と等分布荷重の場合とでは下に述べるように応力図の形が違うので注意が必要です.
①せん断力図の場合
集中荷重の場合はその値が一定ですが、等分布荷重の場合は直線的に変化します.
②曲げモーメント図の場合
集中荷重の場合は直線的に変化し、等分布荷重の場合は2次曲線になります.
また、曲げモーメント図の+の部分には引張力が、-の部分には圧縮力が生じます.
これらの図の違いの数学的意味はSTEP2で説明します. >>Lesson9へ