ここでは図14-1に示すトラスを節点法で解いていきます.
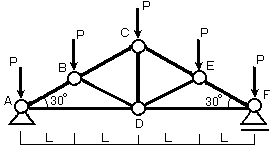
①まず,反力を求めます.
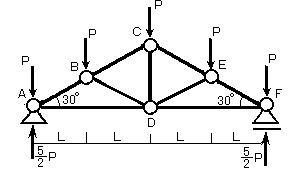
この場合、左右対称の構造物なので反力はピンとローラーで半分ずつ負担します…
![]()
よって図14-2のように反力が生じることになります.
(1)ここではまず、A点について考えます.
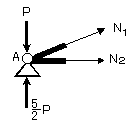
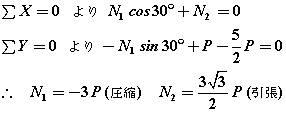
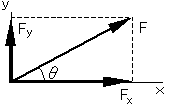
下の図に示す力Fの分力Fx,Fy の値は
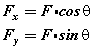
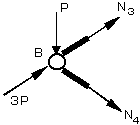
(2)同様にB節点について考えると


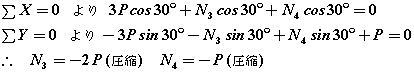
(3)同様にC節点について考えます
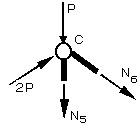
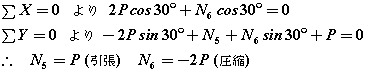
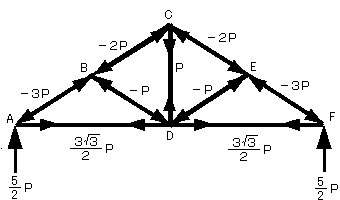 となります
となります >>Lesson15へ