丂師偵丆傕偆侾偮偺僩儔僗偺夝朄偱偁傞乽愗抐朄乿偵偮偄偰妛廗偟傑偟傚偆丏
丂愗抐朄偼丆擟堄偺晹嵽偺幉曽岦椡傪媮傔傞応崌偵桳岠側曽朄偱偁傞偲偄偊傑偡丏偟偨偑偭偰丆僩儔僗晹嵽慡偰偺墳椡偑
抦傝偨偄応崌偼乽愡揰朄乿丆僩儔僗峔憿偺擟堄偺晹嵽偺墳椡偺傒抦傝偨偄応崌偼乽愗抐朄乿偲巊偄暘偗偰夝偔曽偑娙堈偱偟傚
偆丏
愗抐朄偵偼丆愗抐柺偺偮傝偁偄忦審幃偲偟偰丆嚁倃亖侽丆嚁倄亖侽丆嚁俵亖侽 傪梡偄偰晹嵽偺幉曽岦椡傪媮傔傞曽朄偱
偁傞乽
僇儖儅儞朄乿偲丆摨堦捈慄忬偵側偄擟堄偺俁愡揰偺傑傢傝偺儌乕儊儞僩偺偮傝崌偄偐傜媮傔傞曽朄偱偁傞乽儕僢僞乕朄乿
偑偁傝傑偡丏
丂丂丂丂
偲側傝傑偡丏
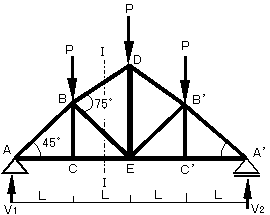
嘇師偵丄墳椡傪媮傔傛偆偲偡傞晹嵽偺偁傞売強偱僩儔僗傪壖偵愗抐偟傑偡丏偙偺帪愗抐偡傞晹嵽悢偑俁嵽埲壓偲側傞傛偆偵偟傑偡丏 塃偺応崌嘥亅嘥偺晹暘偱愗抐偟偰抐柺椡偺偮傝崌偄傪峫偊偰偄偒傑偡丏偙偺帪丄愗抐柺偺晹嵽偺墳椡傪堷挘椡偲側傞傛偆偵壖掕偟傑偡丏乮壓恾傪嶲徠偺偙偲乯
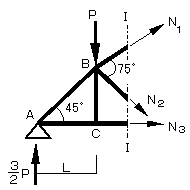
儌乕儊儞僩偺偮傝崌偄幃傪棫偰傞応崌丄婎弨偵偡傞愡揰偼擟堄偱傛偄偺偱偡偑丄堦斒偵偼堦斣寁嶼偑堈偟偔側傞揰偵愡揰傪掕傔傞偺偑椙偄偱偟傚偆丏乮嵍恾偺応崌丆俛揰偺儌乕儊儞僩偺偮傝崌偄傪峫偊偨応崌俹丄俶侾丄俶俀 偺俛揰偵偍偗傞儌乕儊儞僩偺抣偑侽偵側傞偨傔寁嶼偑梕堈偵側傝傑偡乯
丂丂丂丂丂丂丂丂丂丂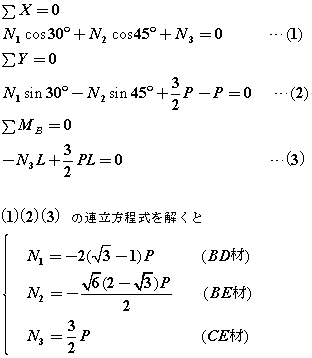
丂丂丂丂丂丂丂丂丂丂偲側傝媮傔傞傋偒俁嵽偺晹嵽墳椡偑偡偖偵媮傑傝傑偡丏
乮俀乯儕僢僞乕朄偵傛傞僩儔僗偺墳椡嶼掕
俠俤嵽偺幉椡傪儕僢僞乕朄偵傛傝媮傔傑偡丏
嘆傑偢斀椡傪媮傔傑偡丏乮偙偺栤戣偺応崌斀椡傪媮傔側偔偰傕俁嵽偺幉椡偼媮傔傜傟傑偡偑堦墳暅廗偺偨傔偵乧乯
丂丂丂
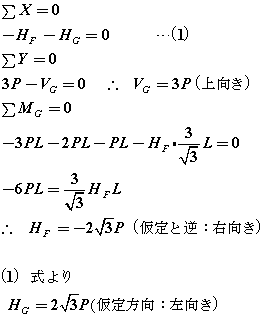
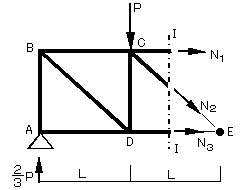
嘇師偵丄墳椡傪媮傔傛偆偲偡傞晹嵽偺偁傞売強偱僩儔僗傪壖偵愗抐偟傑偡丏偙偺帪丄僇儖儅儞朄偲摨條偵愗抐偡傞晹嵽悢偑俁嵽埲壓偲側傞傛偆偵偟傑偡丏 忋偺応崌嘥亅嘥偺晹暘偱愗抐偟偰抐柺椡偺偮傝崌偄傪峫偊偰偄偒傑偡丏偙偺帪丄愗抐柺偺晹嵽偺墳椡傪堷挘椡偲側傞傛偆偵壖掕偟傑偡丏
忋偺傛偆側応崌丆愗抐柺偺嵍懁偱峫偊偨曽偑丆奜椡偺悢偑彮側偄暘寁嶼偑梕堈偵側傝傑偡偺偱丆愗抐柺偺嵍懁偱椡偺偮傝崌偄傪峫偊偰偄偒傑偡丏乮壓恾嶲徠乯
丂丂丂丂丂丂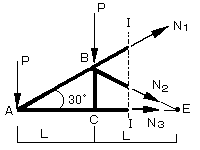
偨偩偟丄僇儖儅儞朄偲偺堘偄偼丄幉椡傪媮傔傞偺偵摨堦捈慄忋偵側偄擟堄偺俁愡揰偺傑傢傝偺儌乕儊儞僩偺偮傝崌偄傪峫偊傞帠偱偡丏乮偮傑傝丆悈暯曽岦丆悅捈曽岦偺椡偺掁傝崌偄偼峫偊傑偣傫丏乯擟堄偺俁愡揰傪峫偊傞応崌偼丆摉慠偦偺揰偵惗偠傞儌乕儊儞僩偺寁嶼偑梕堈偵側傞傕偺傪慖傫偩曽偑椙偄偺偱丆僉儍儞僙儖偝傟傞椡偺悢偑懡偄愡揰傪慖傫偩傎偆偑椙偄傢偗偱偡丏偙偙偱偼丆俙愡揰丆俛愡揰偺傎偐偵俀偮偺枹抦墳椡偺嶌梡慄忋偱岎傢傞愡揰俤傪擟堄偺3愡揰偲偟傑偡丏
丂丂丂
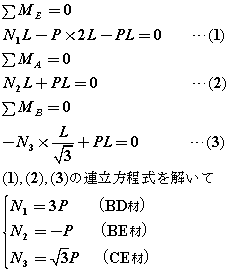
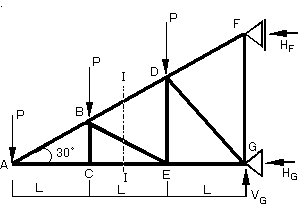
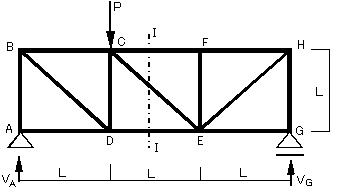
塃偺恾偺傛偆側暯峴尫僩儔僗偺忋尫嵽俠俥丆幬嵽俠俤丆壓尫嵽俢俤偺幉椡傪媮傔傑偡丏
嘆傑偢偼斀椡傪媮傔傑偡丏
丂丂丂丂丂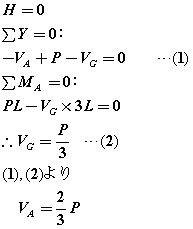
丂丂丂丂丂丂
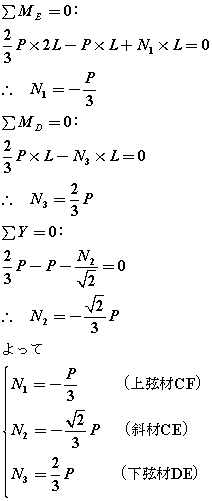
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 >>俴倕倱倱倧値侾俇傊