Ｌｅｓｓｏｎ２０． 断面１次モーメント

断面１次モーメントは、一般に断面の図心（重心）を求めるために必要な係数です。

ある図形の断面積をＡとしたとき、その図心（重心）から、与えられた軸までの距離をｙとすると、その断面１次モーメントＳは次の式で求める。

�@断面図形を、図心の位置が分かるＡ1、Ａ2とに区分する。

�A断面積ＡとＸ軸についての断面一次モーメントＳｘを求める。

　　　　　　　　　　y1,y2 Ｘ軸からＡ１、Ａ２の図心までの距離

�B式（２０−１）からy0を求める。

　以上のことは、Ｙ軸についても同様に求められる。

　部材の曲げに対する強さは、断面の大きさだけでなく、その断面の性質によって定まります。同じ断面の部材であっても、その断面の形状（性質）によって曲げに対する強さは異なってきます。
　そのような曲げに対する断面の性質として、基本となるのが、断面２次モーメントなのです。従って、この断面２次モーメントはよく理解しておく必要があります。
　簡単にいえば、断面２次モーメントが大きくなるほど、曲げに対する強さも増し、断面２次モーメントが小さくなるほど、曲げに対する強さは減るのです。
　その断面２次モーメントは、正確には積分で求められます。

　　　　　　（ｂ：部材の幅、ｈ：部材の丈）

　部材の丈が２倍になると、ｈが８倍の大きさになることから、曲げに対しては部材の幅よりも丈がいかに重要かということがわかります。
　途中の計算式は、それほど重要ではありません。重要なのは、その結果として得られた値です。一般に部材は長方形の断面を採用することが多いので、この断面２次モーメントだけは、いつでも思い出せるように、しっかりと記憶しておいてください。

（図２１−１）

�@全体の断面２次モーメントを求める。

　　　　　　（式２１−１）

�A中空部の断面２次モーメントを求める。

　　 　　　　（式２１−２）

�B求める断面２次モーメントは、（式２１−１）−（式２１−２）

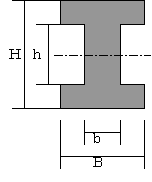
�@さきほどと同様に、全体の断面２次モーメントを求める。

�A中空部の断面２次モーメントを求める。

�B求める断面２次モーメントは