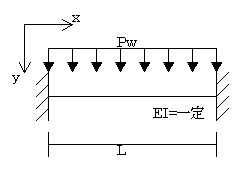
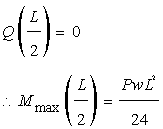ここでは不静定構造物の変形について解説していきます。
Lesson25. 不静定構造物の解法
4回積分してみると次式のようになります。
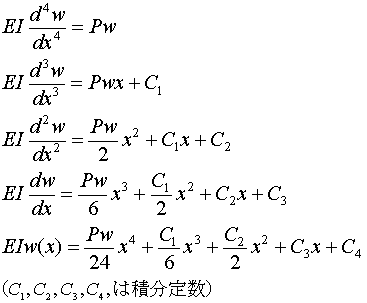
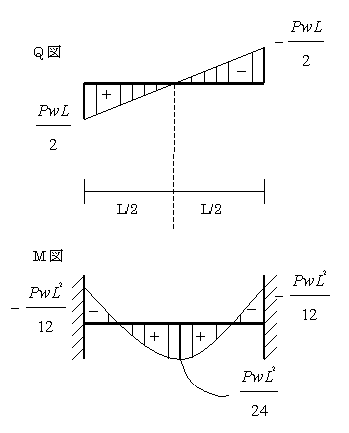
荷重Pwを積分すると、せん断力Q
せん断力Qを積分すると 、モーメントM
モーメントMを積分すると、たわみ角θ
たわみ角θを積分すると、たわみw
になることを覚えておきましょう。
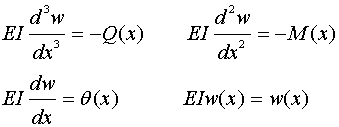
境界条件より
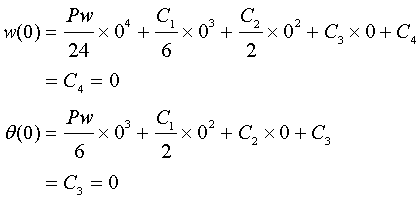
よって次式が得られる。
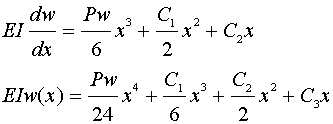
次に境界条件よりM(x)とw(x)の連立方程式を解く
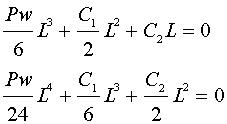
この連立方程式より

が得られる。これで全ての積分定数を求めることができました。よって…
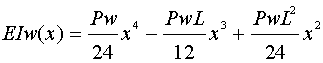
が得られるので、xに(L/2)を代入すると…
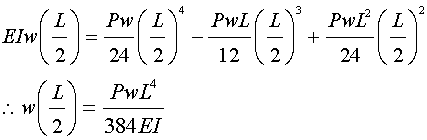
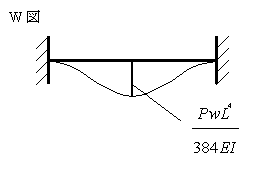
これでたわみの最大値が求められた。次にさきほどの積分定数を代入すると次式が与えられます。
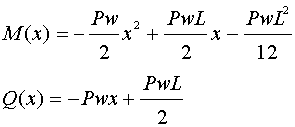
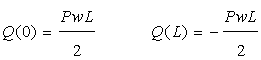
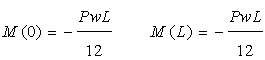
一般にせん断力の値が0となる点で曲げモーメントは最大になるので…