丂偙偙偱偼丄愭偺俴倕倱倱倧値侾侾偱妛傫偩丄椑偺旝暘曽掱幃偺巊偄曽偵偮偄偰丄夝愢偟偰偄偒傑偡丏
丂椑偺旝暘曽掱幃傊偺棟夝偑傛傝怺傔傜傟傞傛偆丄恾侾俀亅侾偵帵偡傛偆偵丄愭偺俴倕倱倱倧値侾侽偱庢傝忋偘偨丄扨弮椑偵偮偄偰峫偊傑偡丏
丂嵗昗宯偼塃偺傛偆偵掕傔傑偡丏
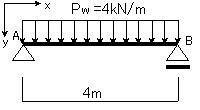
丂忋偺恾偱丄摍暘晍壸廳側偺偱丄僗僷儞偑曄壔偟偰傕丄偦偺抣丂偼忢偵堦掕偱偁傞偺偱丄俹倵亖係kN/m乮掕悢乯偲偟傑偡丏
嘇丂師偵椑偺旝暘曽掱幃傪愊暘偟偰丄偣傫抐椡俻乮倶乯丄嬋偘儌乕儊儞僩俵乮倶乯偺幃傪媮傔傑偡丏
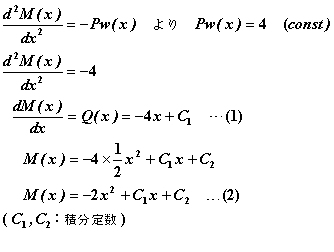
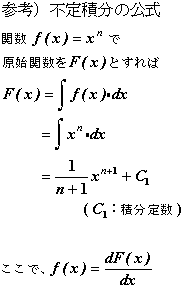
|
巟揰偺庬椶
|
儘乕儔乕 |
僺丂儞 |
屌掕抂 |
|
|
嫬奅忦審
|
俵乮倶乯亖侽
倵乮倶乯亖侽 |
俵乮倶乯亖侽
倵乮倶乯亖侽 |
倵乮倶乯亖侽
兤乮倶乯亖侽 |
俻乮倶乯亖侽
俵乮倶乯亖侽 |
倶亖侽乲俵乮侽乯乴偺帪丗俵亖侽
倶亖係乲俵乮係乯乴偺帪丗俵亖侽丂偲俀偮偺嫬奅忦審傪帵偡偙偲偑偱偒傑偡丏
乮俀乯幃偱媮傔傞愊暘掕悢偼俠侾丄俠俀偺俀偮偱偁傞偺偱 丄忋偵帵偡傛偆偵俀偮偺嫬奅忦審偑寛傑傟偽丄俠侾丄俠俀偺抣偼堦堄揑偵寛掕偝傟傞帠偑暘偐傝傑偡丏
丂傛偭偰丄愊暘掕悢俠侾丄俠俀傪媮傔傞偲乧
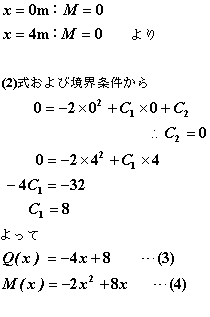
偲側傝丄乮俁乯丄乮係乯幃偼俴倕倱倱倧値侾侽偱椡偺掁傝崌偄偵傛傝媮傔偨幃偲摨偠幃偵側傞偙偲偑暘偐傝傑偡丏
埲忋偑丄旝暘曽掱幃傪巊偭偰椑傪夝偒曽偱偡丏偙偺偲偒曽偱夝偔偙偲偺棙揰偼丄夝偄偰傒偰傕傜偆偲暘偐傞偺偱偡偑丄乽斀椡傪媮傔側偔偰傕椑偑夝偗偰偟傑偆乿偙偲偱偡丏嶌梡偟偰偄傞壸廳偺娭悢偲嫬奅忦審偝偊寛傑傟偽丄偁偲偼娙扨側愊暘偱墳椡恾偑昤偗偰偟傑偆偺偱偡偐傜丄旕忢偵憗偔夝偔帠偑偱偒傑偡偺偱丄偤傂棟夝偟偰偍偒傑偟傚偆丏
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂>>俴倕倱倱倧値侾俁傊