Lesson10.力の釣合いによる解法（２）
　 次に、等分布荷重が作用する図10-1に示すような梁を解いてみましょう．


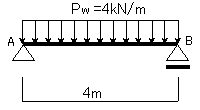
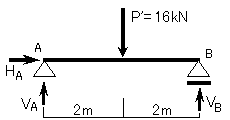
①　まず、Ｌｅｓｓｏｎ９と同様に反力を求めます．（反力の仮定は図１０－２のようになります．）		 （図１０－１）

※等分布荷重なので、反力を求める場合は、集中荷重に置き換えます．忘れてしまった人はＬｅｓｓｏｎ７を確認して下さい．
集中荷重に置き換えると、下の図のようになります．

（図１０－２）
 
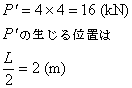
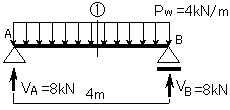
よって反力は下の図のようになります．
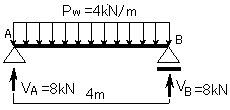
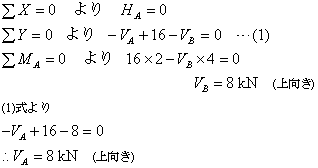
②　次に、下図のように、等分布荷重が作用している部分の任意の距離（ｘ）で切断し、その部分での力の釣り合いを考えます．（図１０－３）   （図１０－３）
切断面①での力の釣り合い

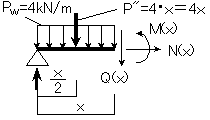
分布荷重が作用する場合の切断面での力の釣合い
　一般に、分布荷重（Ｐｗ）の作用している梁を切断法で考える場合，支点から切断面までの任意の距離（ｘ）に対して、分布荷重（Ｐｗ）が作用しているので、切断面における力の釣合いを考える場合、分布荷重を集中荷重に置き換えて、計算しなければなりません．（図１０－３）		  

□切断面①での力の釣合□

 		   
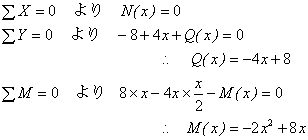
　左の計算結果から、等分布荷重が作用する場合のせん断力Ｑ（ｘ）はスパンｘについての１次関数、曲げモーメントＭ（ｘ）はスパンｘについての２次関数で表せる事が分かります．集中荷重の場合、曲げモーメントの直線を表す式は、載荷点により異なりますが、分布荷重の場合は、分布荷重が作用している区間内であれば、Ｑ（ｘ）とＭ（ｘ）の式は１つずつで、せん断力と曲げモーメントの変化の様子をあらわすことができるのです．つまり、左のＱ（ｘ）、Ｍ（ｘ）の式に任意のスパン長（ｘ）の値を代入すれば、せん断力と曲げモーメントの値が直ちに求められます．
　また、分布荷重が作用する場合であれば、曲げモーメントの式を求めれば、せん断力の式は、力の釣合条件を用いずとも、数学的に求めることができます．逆も同様で、せん断力の式がわかれば、曲げモーメントの式は、力の釣合いを使わなくても求められます．このことについては、次のＳＴＥＰで学んでいきます．
　応　力　図
計算結果を整理しておくと…

  
よって応力図は下のようになります．
　梁の解き方のまとめ

Ｌｅｓｏｏｎ９，Ｌｅｓｓｏｎ１０で梁の解き方を学びました．
静定梁の解き方の順序についてまとめておくと下のようになります．

① 反力を求める．

②　応力を求める位置より左側（または右側）の外力と、仮定した応力との力の釣り合いを考える．

③　このとき応力を求める位置に、各応力を正の向きに仮定する．

④　求めた応力を元に、各応力図を描く．
              　　　　　　　　　　>>Ｌｅｓｓｏｎ１１へ