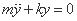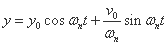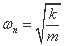「地震の後、
天井から吊り下げられた電灯がしばらく揺れていた」という現象。
これは誰でもよく経験した事があると思います。
右の図のボタンでその様子が見られます。
確かめて見て下さい。
この「地震の後の電灯」のように、
力が作用していなくても自由に振動している現象を“自由振動”といいます。
自由振動しているものに更に力を作用させたら、
どのようなことが起こるでしょう。
力のかけ方によっては、
ほんの小さな力で構造物が大きく揺れるという、
“共振現象”が生じる事もあります。
ここに述べる自由振動は振動を学ぶ上で最も重要な概念であり、
ここで求められた事項は後にもよく利用されます。
自由振動の力学モデルとその釣合式は、簡単なもので次のように表せます。
文字の上の点は、時間 t で微分した回数を表します。
y は変位、y の上に点が 2 つは加速度を表しています。( y
の上に点が 1 つは速度です。)
左辺は先に説明した慣性力と復元力、右辺は「手を放した」状態なので力がかかっていないということで、
その合計は 0 になります。
イメージしにくい場合は、釣合の様子を表したこちらの絵を見てみて下さい。
このモデルは、言い換えると
「質量を考えない柱と質量 m の梁」
とも言えます。
自由振動をしているボールの変位 y を求める式は、次のように表せます。
y0 は初期変位、v0
は初速度、ωnは固有角振動数を表しています。
例えば「ある所までボールを引っ張っておいて、そこからただ放すだけ」という振動を計測する時、
放す位置が y0 、初期速度 v0 は 0 ということになるので、
この自由振動の動きと変位は下の絵のようになります。
ボールが 1 番右に来ている時が、初期変位であり最大変位でもある y0 です。
初期速度が 0 なので、1 つ上の式の v0 / ωn ・ ( sin ωn t ) は 0 になっています。
ここまでで、固有角振動数ωn や、固有周期 Tn
といった値が出てきました。
次は、これらの値について説明していきます。
固有角振動数 ωn は、文字通り「その系の固有の角振動数」です。
建物なら建物ごとに、質量とばね定数があります。
その質量やばね定数によって決まる、“時間2π内で何回振動するかを表す量”が、固有角振動数です。
ばね定数 k が大きく質量 m が小さければ、固有角振動数
ωn の値は大きくなりますね。
つまり、“下が強くて上が軽いラーメンは速く揺れる”とも言えます。
また、固有角振動数 ωn から、固有振動数 fn
と固有周期 Tn を求めることが出来ます。
ちなみに固有振動数とは 1 秒間に振動する回数、固有周期とは 1 回振動するのにかかる時間です。
各値は次のような関係になっています。
固有角振動数 ωn が大きくなると、
固有振動数 fn は比例して増加し、
固有周期 Tn は反比例して短くなります。
そして、グラフの山が来るテンポ、つまり揺れるスピードが速くなっていきます。
ここまで出てきた各値を使って、建物がどのように揺れるかを見てみましょう。
モデルは柱のばね定数を k [ N / m ] 、梁を剛( k = ∞ )、梁の質量を m [ kg ] 、
初期変位 y0 = 1 [ m ] とした時の、1 層ラーメンです。