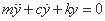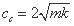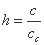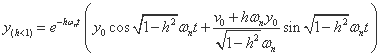CHAPTER4　減衰振動

これまでの自由振動では、
一旦振動が生じるとずっとその揺れは続いていました。
しかし、普段の生活の中で経験する振動は、
時間が経つと次第に揺れ幅が狭まり、最後には停止しますよね。
実生活では構造物以外に、映画館のドアなどによく見かけるので、
それをイメージすると考え易いと思います。

このように徐々に振幅が小さくなる振動を“減衰振動”と言います。

減衰力には次の3段階の特性があるといわれています。

①遅い速度　　　　　 →　速度に比例
②中程度の速度　　 →　速度の2乗に比例
③速い速度　　　　　→　速度の複雑な関数

揺れる速さが速ければ速いほど、それを止めようとするブレーキ力（減衰力）も急速に大きくなります。
しかし、構造物の振動は、比較的遅い速度の振動と考えることができるので、
構造物の減衰力は①「速度に比例」するパターンが当てはまります。

一般に、このように速度に比例する減衰力を、「粘性減衰」と呼びます。
また、この種の減衰力は次式で示される“ダッシュポット”というモデルで表されます。

ダッシュポットのモデルが分かりにくい方は、
水の入ったなべに、一回り小さいサイズのなべのふたを浮かべた物を想像してみて下さい。

ふたを下に力強く押すと大きな水の抵抗を感じますが、
ゆっくり押せば意外と簡単に沈められるという感覚があると思います。

また、ふたがぎりぎりはまるほどの大きなサイズなら減衰係数 c は大きく、
なべの半分ほどしかない小さなふたなら減衰係数 c も小さくなるということが言えます。
これが速度に「比例する」ということで、構造物の揺れが収まっていく時もこのような力が働いています。

ちなみに減衰係数 c の大きさは、部材内部の摩擦抵抗や空気抵抗などが複雑に関係しあって決まります。

先に説明した考え方を踏まえて、減衰振動系の力学モデルを考えると、力の釣合は次のようになります。

自由振動の方程式に、さらに減衰力 cy（.） を加えて考えています。

この減衰力 cy（.） が振動系全体に与える効果は、質量 m とばね定数 k によって代わってきます。
同じ減衰力 cy（.） のダッシュポットをオートバイに使用した場合と、ダンプトラックに使用した場合では、
減衰効果が代わってくるというのを想像してみると、分かり易いと思います。
そこで、まずは質量 m とばね定数 k に関連した標準の減衰量 c_c を定めます。

標準の減衰量 c_c は微分方程式を解いて導かれています。
微分方程式の解き方を調べたい方は、
ゼミのホームページのこちらでテキストをダウンロードするなどして調べて下さい。
そして、これまでの減衰係数 c を標準の減衰量 c_c で割った値 h を用いて次のように表します。

この h を“減衰定数”と呼びます。
減衰定数 h は、減衰係数 c よりも、その振動系を表す固有の量として適しています。
よって今後、減衰効果を表す量は、この減衰定数 h を使っていきます。

減衰定数 h のとる値によって、
振動の仕方は大きく3パターンに分けることができます。
（先の 5-1　減衰モデル の項で述べた3つの性質とはまた違うものです。）

①　h > 1 の場合　→　過減衰
標準の減衰量 c_c より減衰係数 c が大きい時、
つまり、減衰定数 h > 1 の状態を“過減衰”と呼びます。
一般構造物の振動では、過減衰になることはほとんどありません。

過減衰の特徴は、揺れないことです。
それぐらい減衰力が強いのです。
普通の振動は上下であったり左右であったり、往復運動になります。
しかし、過減衰の場合は反対側へは行かずに、
釣り合う点、つまり平衝点へゆっくり近づいていって止まります。

②　h = 1 の場合　→　臨界減衰
c_c と c が同じ時の減衰の状態を、 “臨界減衰”と呼びます。
これも基本的には過減衰と同じで、何度も揺れたりはしません。
つまり、c_c とは、臨界減衰を示す量だったわけです。

しかし変位が 0 になるスピードは速く、
振動するかしないかのギリギリのスピードでサッと 0 地点に戻ってきます。

③　h < 1 の場合　→　減衰振動
振動しながら徐々に振幅が収まっていくのがこの“減衰振動”で、
一般の構造物の振動はほとんどがこの振動です。

h が小さければ小さいほど、自由振動のように振動が長く続きます。

実際の構造物で考えると、鉄骨構造の建物は内装材があると 0.03 、
ナゴヤドームや立体駐車場などのように鉄骨が剥き出しになっているものは、
0.01～0.02 ぐらいになっています。

鉄筋コンクリートの建物は、大体どれも 0.05 ぐらいです。

「地震が収まった後もしばらくは建物が揺れ続けていた」という経験を思い出して頂ければ、
建物の減衰定数がこれぐらい小さいというのもなんとなく分かって頂けると思います。

この時の変位 y を表す式は、①～③それぞれで変わってきます。
③の減衰振動の場合は、初期変位を y₀ 、初期速度を v₀ とすると、
次のような式になります。

下のモデルでここまで学んだことを復習できるようになっているので、
色々な値を操作して試してみて下さい。

減衰の程度を表すものとして、減衰定数以外に対数減衰率 δ と呼ばれるものがあります。

減衰振動のグラフでは時間が経つごとに山の大きさが小さくなっていきます。
（CHAPTER4 の自由振動は h = 0 としてあるので、
　山の大きさは変わっていません。）
そして、その山ごとの最大変位を大きい方から Y₁ 、Y₂ 、Y₃ とつけていくと、
対数減衰率 δ は次の式で表されます。