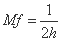CHAPTER5　定常振動

定常振動の場合、外力の角振動数 ω と、構造物の固有角振動数 ω_n の関係によっては、
揺れが数100倍にも増大する“共振”状態になることもあります。

ちなみに、“地震”や“風”などによる振動は、非定常で過渡的なものなので、
「非定常振動」「過渡振動」「不規則振動」などと呼びます。
これは次の CHAPTER7 非定常振動で扱います。

一定の周期外力 P₀sinωt が作用する振動系は次のようなモデルと式で表されます。

ここでの ω は外力の角振動数で、固有角振動数 ω_n とは違います。

定常振動状態の振幅特性（振幅 y の変化の仕方のこと）は、
外力による振動の角振動数 ω と、建物の固有角振動数 ω_n の比によって変わってきます。また、CHAPTER 4 で学んだ減衰定数からも影響を受けます。 振幅特性はグラフを用いて説明すると分かりやすいので、まずは下のグラフ「変位共振曲線」を見て下さい。

グラフ縦軸の拡大率は、
動的外力 P₀sinωt による質量 m ・ダッシュポット c ・ばね k の振幅 y₀ （上で表した図による変位）と、
静的外力 P₀ による変位 y_st （ CHAPTER 3 ばねの最初で示した公式）との比、 y₀ / y_st です。
次のような式で表されます。

拡大率 y₀ / y_st が大きいということは、
時間が経つにつれどんどん振幅が大きくなっていくということになります。
ではグラフが表す特性を左のゾーンから順に見ていってみましょう。

① ω / ω_n < 1 の範囲では、外力の振動数 ω の値が増加すると、拡大率も増加しています。
この時は、建物の振動に比べて外力がゆっくりと変化していることを表しています。
上に表示されている矢印アニメの、動きが遅くなったものをイメージしてみて下さい。

② ω と ω_n がほぼ等しい時、減衰定数 h が小さければ、拡大率のピークはとても大きくなります。
振幅がこのように大きくなる状態を“共振”と呼びます。
共振状態は、振動している建物にとって非常に危険な状態です。

また、このピークの時（ ω / ω_n = 1 ）の拡大率を共振倍率 M_f と言います。
上の式の ω / ω_n に 1 を代入したのが共振倍率 M_f です。
この式はとても簡単なので覚えておきましょう。

共振倍率 M_f は、減衰定数 h によってのみ左右されるので、
質量 m や、ばね定数 k をどのように変更しても変わりません。
最近の溶接鋼構造物は減衰が非常に小さく、共振倍率が 100 倍を超えることも珍しくない為、
注意が必要です。
そう考えると、 CHAPTER 1 の釣鐘の話もあながち冗談でもないということが分かります。

③グラフの右側の方を見て下さい。
ω / ω_n > 1 の範囲においては、 ω が増加すると拡大率が減少します。
ω / ω_n → ∞ となるにつれ、拡大率は 0 に近づいていきます。

この中で最も興味深いのはやはり共振であると思います。
強固な建物でも共振の対策をしていないと、倒れてしまう可能性があります。

日常生活の中で共振に深く関係する現象としては、ブランコが挙げられます。
この場合、ブランコを揺らす人間自体が外力となっています。

ブランコに乗る姿をイメージしてみて下さい。
勢いをつけようとして振り出す足は、自然とブランコの揺れるタイミングに合わせて振り出されているはずです。
これによって、 ω / ω_n が 1 に近づくため、共振が起きて大きな揺れになっていくという訳なのです。