建築物の骨組みは、ほとんどが不静定構造物といっても過言ではない。不静定構造物は、力の釣合条件だけでは、応力を求めることはできないが、部材の変形の状態を考え合わせると、応力を求めることができる。ここでは、部材が曲げられて変形するときに生じるひずみと部材の変形との関係を理解し、部材内に生じる応力と合応力との関係を学ぶ。
 

　Ｌｅｓｓｏｎ２４． 曲げ変形と曲げモーメントの関係

まず、部材の変形を、図芯位置をX方向につなげた直線の変形によって表すことにする。
このX軸上の直線を材軸と呼ぶことにする。

  
                 
図２４−１
             
   
       
  　　　　　　　　　(変形前)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(変形後)
     
    変形を起こす前に、微小な間隔dxの両端に材軸に垂直な平面を二つ描く。この平面を法面と呼ぶ。
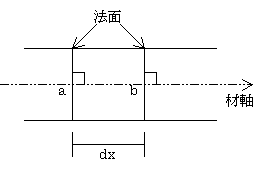
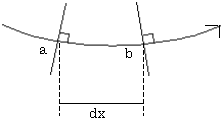
次に、荷重を受け、部材が曲がった後の変形を、この二つの法面が「部材が変形した後も、材軸に垂直でしかも平面を保っている」というオイラー・ベルヌーイの仮定を用いて求める。
オイラー・ベルヌーイ仮定は二つのことを仮定しています。
一つは、変形後の法面が材軸に対し垂直を保つということ。
他の一つは、法面が変形後も平面であることで、この仮定は平面保持とも呼ばれています。

　　（１）梁の曲げ変形とひずみの関係を求める
                   
さきほどの仮定を基にして、梁の曲げ変形とひずみの関係をもとめる。
図２４−２より、変形後の微少部材の両端aとbの法線は一点ｏで交わることがわかる。この点を曲率中心と呼び、図中のρは曲率半径という。図芯上のa点とb点における回転角はθとθ＋dθであり、回転角は、法線が変形後も材軸に垂直であることと、θが微少であることから、図芯の変形wを用いると次の式で表される。
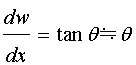　　 　　　 　　　　　　（式２４−１）
またa点とb点の変形後の法線の回転角の差、つまり、回転角の増分量dθは、図２４−２で見られるように、θ−（θ＋dθ）より求められる。また変形後のa点とb点を直線で結んだ線分dsは、角度がラジアン表示であることから、次の式で表される。
　　　　　　　　　　　　　　　　（式２４−２）
部材が大きく曲げられることがない場合、dθが極端に大きくならないとdsとdxにほぼ等しいとしてよいので、上式を次のように書き換えられる。
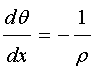　　　　 　　　 　　　　　　　　　（式２４−３）
式２４−１と上式を考慮すると次式が得られる。
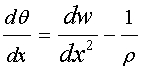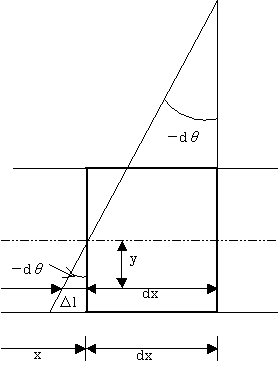
　　 　　　　　　　　　（式２４−４）
次に、断面内のひずみを求めてみよう。ひずみが計算しやすいように、微少断面を図２４−３のように描き変えます。ｙ軸上で正方向の位置ｙにおける軸方向のひずみεxを求めてみる。曲げによって生じるひずみは、次式のようになる。
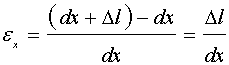　　（式２４−５）
図２４−３より
　　　　　 　　　　　　　　　　（式２４−６）
これを式２４−５に代入すると、ひずみは次式になる。

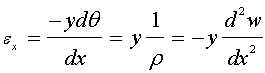
　　　　　　　　　　　　　　　　　　　　　　　　 　　　（式２４−７）
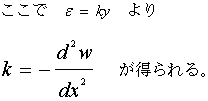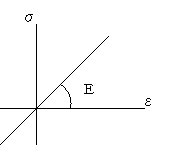
　　　　（式２４−８）
また右図２４−４より、応力は弾性域であり、また、断面は一様な材料であることをかていしているので、次式が成り立つ。これは応力とひずみの関係を表している。
　　　　 　　　　　　　　　　　　（式２４−９）
次に、曲げモーメントを求めてみる。曲げモーメントの定義式より
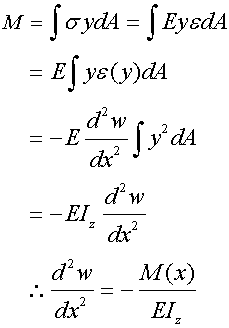（式２４−１０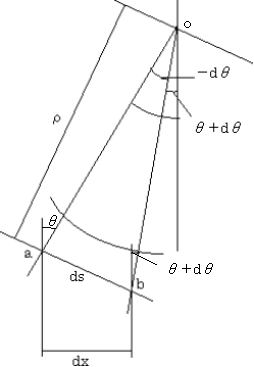）		   図２４−２
           
  図２４−３
 
     
図２４−４
   
                   
                 
上式２４−１０と、Ｌｅｓｓｏｎ１１で求めた力の釣り合い式は、梁理論において最も基本的であり、かつ重要な微分方程式となります。この２つの基本式を用いるとモーメントＭを消去することができ、１つの簡単な微分方程式となります。
まず、式２４−１０の両辺をｘで２階微分します。
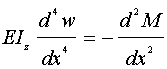　　　　　　 　　　　　　　　（式２４−１１）
次に上式と力の釣り合い式より、モーメントを消去すると、次のように４階の微分方程式が得られる。この微分方程式が、断面が一様である梁の挙動を支配する方程式となる。
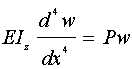　　　　　 　　　　　　　　　　　　　（式２４−１２）		    
                     
            　　　　　　　　　　　　　
　　　　　　　　　　>>Ｌｅｓｓｏｎ２５へ