これまでは、力の釣り合い条件だけを用いて応力を求めることのできる、静定構造物について学んできました。しかし実際は
建物のほとんどが、力の釣り合い条件だけを用いて応力を求めることができない不静定構造物です。そのような不静
定構造物を解く場合用いられる方法として、たわみ角法と固定モーメント法があります。このSTEPではまず、たわみ角法
について説明していきたいと思います。
Lesson26.
たわみ角法の基本公式
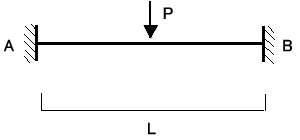
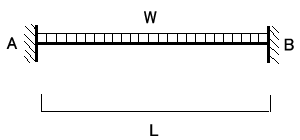
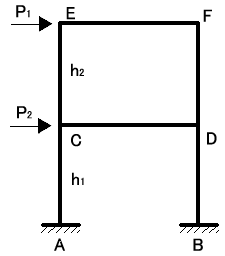
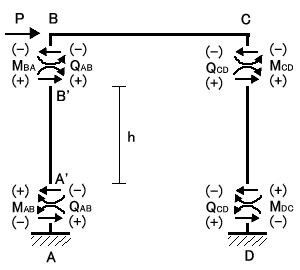
フレームの一部に図7−1のような荷重がかかり、節点A,Bが移動し図7−2のように部材がたわんだとします。このとき材端
A、Bに発生する材端モーメントMAB、MBAを次の様な式で表すことができます。
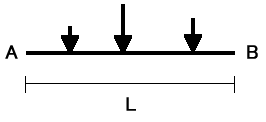
図7−1
 |
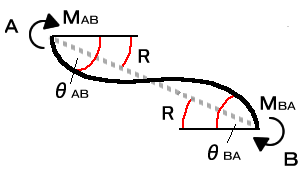
図7−2
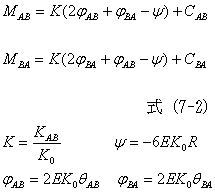 |
一般的には、右辺第一項を標準高度Koで割って2E、
Koを()内にかけて表します。不規則なラーメンでない
場合はこちらのほうが便利です。
?断面二次モーメント? → Lesson21へ
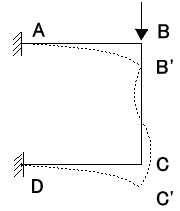
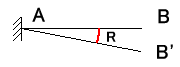
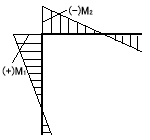
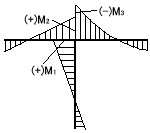
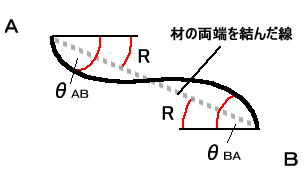 図7−5
図7−5