ＳＴＥＰ７－１ではたわみ角法の基本公式について説明しました。節点の数だけ出てくる節点方程式、層の数だけ出てくる層方程式、 というようにたわみ角法では、多くの方程式を連立させて解くことになります。そのためにまず、 このＳＴＥＰ７－２では実際の流れ、方程式の立て方について説明していきたいと思います。

Lesson27. 手順

右図のような簡単なラーメンを例にして考えていきます

①与えられた条件より、公式中の未知数（θ、φ、ψ、Ｍ、Ｒ）のうち、０となるもの、または互いに等しくなるものを探す

たわみ角：θについて

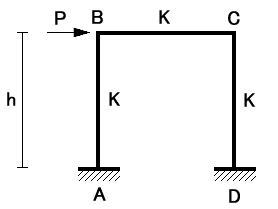
Ａ、Ｄともに固定端　→　θＡＢ＝θＤＣ＝０
すなわち　　　　　　 →　φＡＢ＝φＤＣ＝０
（φＡＢ＝２ＥＫθＡＢ、φＤＣ＝２ＥＫθＤＣ）となります。
節点は直角を保つので
θＢＡ＝θＢＣ　⇒　φＢＡ＝φＢＣ＝φＢ（まとめてφＢとする）
θＣＢ＝θＣＤ　⇒　φＣＢ＝φＣＤ＝φＣ（まとめてφＣとする）

部材角：Ｒについて

はりＢＣの両端は回転しない　⇒　部材角は発生しない　⇒　ＲＢＣ＝０
⇒　ψＢＣ＝０　（ψＢＣ＝-６ＥＫＲＢＣ）
Ｂ点とＣ点の水平方向への節点移動は等しい　⇒　　ＲＡＢ＝ＲＤＣ　
⇒　ψＡＢ＝ψＤＣ＝ψ（まとめる）

②固定端モーメント：Ｃを計算する

③たわみ角法の基本公式を使って方程式を立てる

④節点方程式を立てる

⑤層方程式を立てる

以上の方程式を使ってこのラーメンを解いていくと・・・・
式⑦より、②＋③　４φＢ＋φＣ＋ψ＝０　　...①’
式⑧より、④＋⑤　φＢ＋４φＣ＋ψ＝０　　...②’
①’、②’を連立させて解くと、
φＢ＝-１／５ψ・・・a
φＣ＝-１/５ψ・・・b
Ｐ・ｈ　式⑨を整理して
Ｐ・ｈ/Ｋ＋３φＢ＋３φＣ＋４ψ＝０
これに式a、bを代入して整理すると
ψ＝－５Ｐｈ／１４Ｋ・・・ｃ
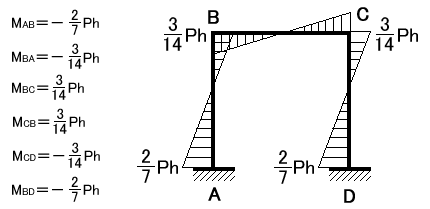
式ａ、ｂ、ｃを①②③④⑤⑥に代入してモーメントを求めることができます。