これまでは、力の釣り合い条件だけを用いて応力を求めることのできる、静定構造物について学んできました。 しかし実際は建物のほとんどが、力の釣り合い条件だけを用いて応力を求めることができない不静定構造物です。 そのような不静定構造物を解く場合用いられる方法として、たわみ角法と固定モーメント法があります。 このSTEPではまず、たわみ角法について説明していきたいと思います。
フレームの一部に図7-1のような荷重がかかり、節点A,Bが移動し図7-2のように部材がたわんだとします。 このとき材端A、Bに発生する材端モーメントMAB、MBAを次の様な式で表すことができます。
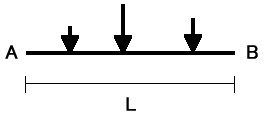
図7-1
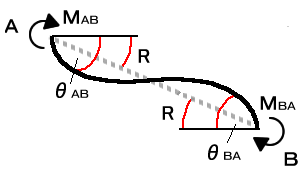
図7-2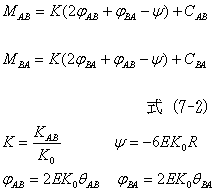
一般的には、右辺第一項を標準高度Koで割って2E、Koを()内にかけて表します。
不規則なラーメンでない場合はこちらのほうが便利です。
図7-3のように部材が荷重を受け、節点(B点、C点)が移動して変形したとします。この時図7-4のように、 材の両端を結んだとき、元の位置との角度を部材角と言います。部材角は節点が移動したときのみ発生します。 なので節点が移動しなかった場合、R=0となります。式(7-2)よりψ=-6EKRだから ψ=0となります。
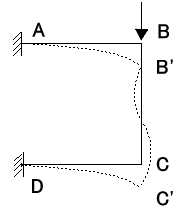
図7-3
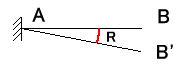
図7-4
図7-5のように部材ABが荷重を受け,たわんでいます。このとき材軸のわん曲線と、 元の位置との角度を節点回転角(たわみ角)といいます。固定端ではたわみ角は発生しない (Lesson12へ)ので、θ=0となります。 式(7-2)よりφ=2EKθだからφもφ=0となります
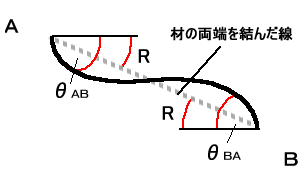
図7-5
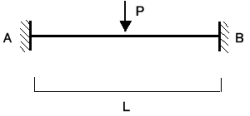
固定端モーメントとは求める材の両端の節点回転角が0のとき、すなわち両端が固定端のときの支点に生じる反力モーメント のことです。基本的な例を下に示します。
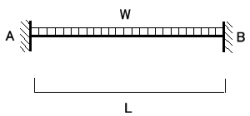 |
 |
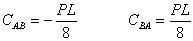 |
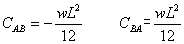 |
複数の部材が接している点、節点には各材の材端モーメントが集まります。これらはすべて 釣り合ってなければなりません。すなわち各接点でのモーメントの合計、ΣM=0を表したのが節点方程式です。
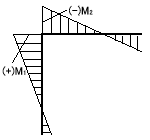
M1+M2=0
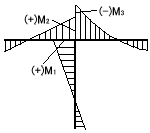
M1+M2+M3=0
各層(各階)における柱のせん断力は、その層から最上階までの間に作用する外力の水平分と釣り合ってなければなりません。
ということは各層でΣX=0という式が成り立つので、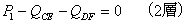
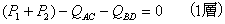
となります。またせん断力Qは
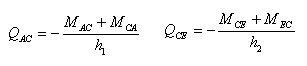
と表すことができるので、これを代入し変形すると
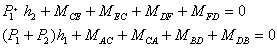
これを層方程式といいます。
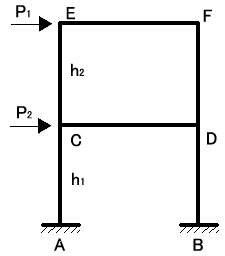
図7-10
↓
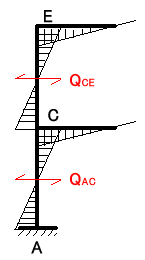
図7-10
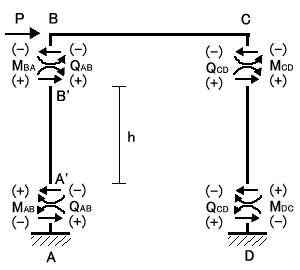
図のように材端に極めて近い場所で応力を仮定したとします。A’、B’に注目して
B’点回りのモーメントの釣り合いを考えると
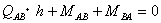
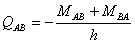
となります。よってせん断力は、その材端にかかるモーメントの和をスパンで割って表すことができます。