先にも学んだように、荷重が作用すると構造物には反力が生じ、それに伴って応力が生じます。 言い方を替えれば、応力は荷重の関数になるといえます.荷重と応力間の数学的関係がわかれば応力を求める場合に、非常に有利になります。 そこで、ここでは荷重と応力の数学的関係について考察してみる事にします。
今、図11-1に示すような、分布荷重 Pw が生じる梁について、任意の微小なスパンdx 部分を取り出して力の釣合いを考えます。この時、構造物は外力に対して構造物は崩壊せずその 形を保っている(釣り合い状態にある)ものとします。
(図11-1)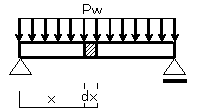
図11-2に取り出した断面における力の関係を示します。
①面(ピン支点より x 離れた面)には、それぞれ応力として、せん断力Q、曲げモーメントMが生じていることになります。
(軸方向力Nについては水平荷重が作用していないので考慮しません)
②面( ①断面より dx だけ離れた面)の応力は、左側より dx だけスパンが増加していますから、せん断力、曲げモーメントともに dQ、dM だけ増加することになります。
左の図でx、yは座標軸の正方向を示します.水平、垂直の力の向き(正・負)はそれぞれこの座標に従うものとします
(図11-2)
微小断面における断面力と荷重の関係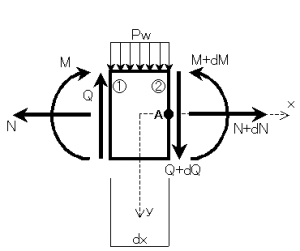
図11-2における力の釣り合いを考えます。まず、取り出した微小距離dxの範囲に分布荷重Pwが生じているので、これを集中荷重に置き換えると…
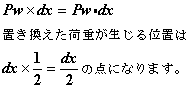
よって下に示す、図11-3の状態で力の釣り合いを考えていきます。
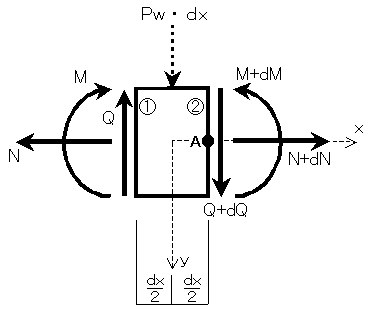

以上より、一般的に、構造物に分布荷重 Pw が作用する場合、次のことが言えます。
構造物に分布荷重が作用する場合、
その曲げモーメントを2回微分した値は、作用する荷重の逆符号の値に等しい。もっと、噛み砕いていえば、「曲げモーメントを
2回微分すると荷重になる」となります。 構造物を解く場合は、そのほとんどが荷重が既知で応力を求める場合が多いので、(4)式から…
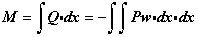
となり、荷重を2回積分すればモーメントの値が導かれます。
(4)式は、一般に「梁の微分方程式」などと呼ばれ、非常に重要な式ですので、なぜ(4)式が導かれるのか良く確認しておきましょう。
この式を使うにあたってのポイントは「分布荷重を関数として捉える」ということです
つまり、等分布荷重ではPw=定数、等変分布荷重ではPw=ax+b(一次関数)として捉える事が
この式を上手く使うポイントになります。先に等分布荷重が生じる梁の曲げモーメント図は2次曲線(放物線)
になる事を学びましたが、この理由はすべて(4)式に起因するのです。等分布荷重が生じるときの曲げモーメントの値は…
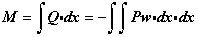
となり、モーメント(M)はxについての2次式、せん断力Qはxについての一次式となり、
M図が2次曲線、Q図が1次直線となる理由が、数学的に説明ができるのです。
また、(4)式はモーメント図の軌跡が1つの式で表す事ができる場合に成り立つといえるので、(4)式が有効に使える場合 というのは以下の3つの場合であるといえます
これは形式的なことですが、荷重をスパンの関数として捉えるということは、それを積分して得られる、せん断力、
曲げモーメントの値というのも当然スパンの関数という事になります。よって数学で用いる関数の記号y=f(x)を参照して、
荷重、せん断力、曲げモーメントをそれぞれPw(x)、Q(x)、M(x)と表記する事にします。
よって梁の微分方程式を再記すると…
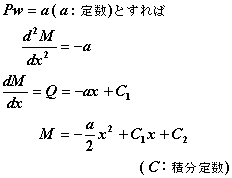
となります。実際に(4)式を使って解く方法は次のLesson12で説明します。
ここでは、先のLesson11で学んだ、梁の微分方程式の使い方について、解説していきます。
梁の微分方程式への理解がより深められるよう、図12-1に示すように、
先のLesson10で取り上げた、単純梁について考えます。
座標系は右のように定めます。
(図12-1)
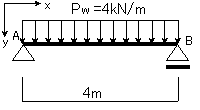
①まず作用する荷重を関数として捉えましょう。
上の図で、等分布荷重なので、スパンが変化しても、その値は常に一定であるので、Pw=4kN/m(定数)とします。
②次に梁の微分方程式を積分して、せん断力Q(x)、曲げモーメントM(x)の式を求めます。
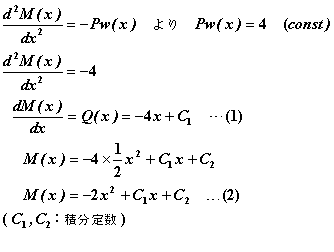
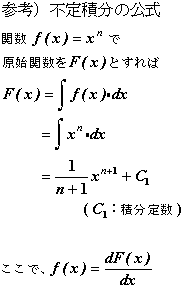
③次に「境界条件」を考えます。境界条件とは簡単に言えば、上の式の積分定数Cを求めるための条件です。 一般に、境界条件は支点の支持条件により決定されます。下の表に支点とその境界条件について示します。
| 支点の種類 |  ローラー |
 ピン |
 固定端 |
 自由端 |
|---|---|---|---|---|
| 境界条件 | M(x)=0 w(x)=0 |
M(x)=0 w(x)=0 |
w(x)=0 θ(x)=0 |
Q(x)=0 M(x)=0 |
※表中で、w(x)とは構造物に荷重が作用した時に生じる「たわみ」を、θ(x) はたわみ曲線の接線と支点とを結んだ角度である「たわみ角」をさします。
図12-1の場合、x=0の点でピン支持、x=4mの点でローラー支持となっていますので、境界条件は
x=0〔M(0)〕の時:M=0
x=4〔M(4)〕の時:M=0
と2つの境界条件を示すことができます。
(2)式で求める積分定数はC1、C2の2つであるので、上に示すように2つの境界条件が決まれば、
C1、C2の値は一意的に決定される事が分かります。
よって、積分定数C1、C2を求めると…
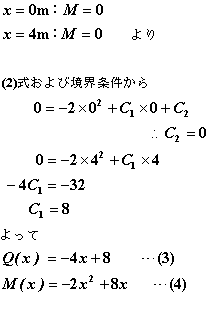
となり、(3)、(4)式はLesson10で力の釣り合いにより求めた式と同じ式になることが分かります。
④ あとは、上で求めた式を元に応力図を描くだけです。
以上が、微分方程式を使って梁を解き方です.このとき方で解くことの利点は、解いてみてもらうと 分かるのですが、「反力を求めなくても梁が解けてしまう」ことです。作用している荷重の関数と境界条件さえ決まれば、 あとは簡単な積分で応力図が描けてしまうのですから、非常に早く解く事ができますので、ぜひ理解しておきましょう。