次に、等分布荷重が作用する図10-1に示すような梁を解いてみましょう。
① まず、Lesson9と同様に反力を求めます。(反力の仮定は図10-2のようになります。)
※等分布荷重なので、反力を求める場合は、集中荷重に置き換えます。忘れてしまった人はLesson7を確認して下さい。
(図10-1)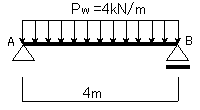
(図10-2)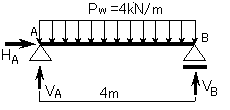
集中荷重に置き換えると、下の図のようになります。
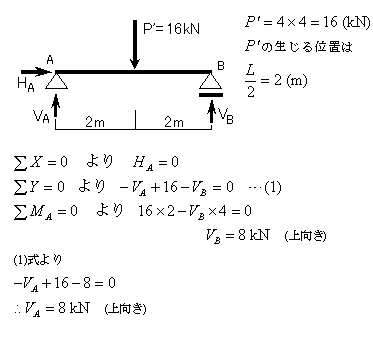
よって反力は下の図のようになります。
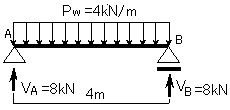
②次に、下図のように、等分布荷重が作用している部分の任意の距離(x)で切断し、
その部分での力の釣り合いを考えます。(図10-3)
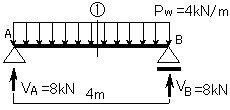
(図10-3)
切断面①での力の釣り合い
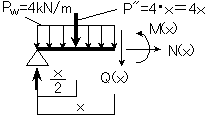
一般に、分布荷重(Pw)の作用している梁を切断法で考える場合、支点から切断面までの任意の距離(x)に対して、 分布荷重(Pw)が作用しているので、切断面における力の釣合いを考える場合、分布荷重を集中荷重に置き換えて、計算しなければなりません。(図10-3)

上の計算結果から、等分布荷重が作用する場合のせん断力Q(x)はスパンxについての1次関数、 曲げモーメントM(x)はスパンxについての2次関数で表せる事が分かります。集中荷重の場合、 曲げモーメントの直線を表す式は、載荷点により異なりますが、分布荷重の場合は、分布荷重が作用している区間内であれば、 Q(x)とM(x)の式は1つずつで、せん断力と曲げモーメントの変化の様子をあらわすことができるのです。 つまり、上のQ(x)、M(x)の式に任意のスパン長(x)の値を代入すれば、せん断力と曲げモーメントの値が直ちに求められます。 また、分布荷重が作用する場合であれば、曲げモーメントの式を求めれば、せん断力の式は、力の釣合条件を用いずとも、 数学的に求めることができます。逆も同様で、せん断力の式がわかれば、曲げモーメントの式は、力の釣合いを使わなくても 求められます.このことについては、次のSTEPで学んでいきます。
計算結果を整理しておくと…
よって応力図は下のようになります。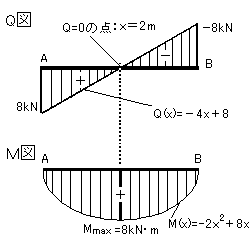
Lesson9,Lesson10で梁の解き方を学びました。静定梁の解き方の順序についてまとめておくと下のようになります。