この部屋では、静定構造物の解析を行う上で最初の段階となる反力について学んでいきます。
構造物に荷重が作用した場合,構造物全体は構造物に作用した荷重と、それに対応して支点に生じる力とが釣り合っていなければ、
構造物は静止して建っていることはできません。
この作用荷重に対応して支点に生じる力を反力といいます。
支点については、Lesson2で学びましたが、支点の構造は、構造物を安全に支えるために 支持部分の移動や回転を拘束しています。つまり、構造物を拘束することによって反力が生じることになります。
図6-1)支点に生じる反力
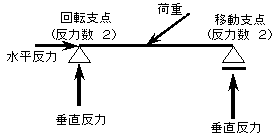
支点に生じる反力の数は、3種類の支持法によって、図のようになります。
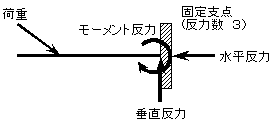
反力の大きさ、方向と向きは、作用する荷重や支点の種類から、右に示す力の釣合条件により求めます。
では実際に構造物に生じる反力を計算してみましょう。
<力の釣合条件>
部材の支点に生じる力の合力が0であると共に、任意の点に対する力のモーメントが0であること。
ΣX=0 (水平方向の力の和が0)
ΣY=0 (垂直方向の力の和が0)
ΣM=0 (支点に生じるモーメントの和が0)
(例題1)図7-1に示すような単純梁に等分布荷重w=2kN/mが作用しているとき、この梁に生じる支点反力を求めなさい。
(図7-1)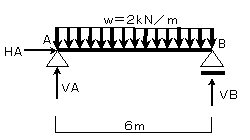
P’の作用する位置は梁の長さ(スパン)の1/2の点になるので、3mとなります。つまり(図7-2)に示す梁と同じ状態です。 よって、図7-2の状態で反力を求めれば図7-1の梁で求めることと同じ事を意味します。
(図7-2)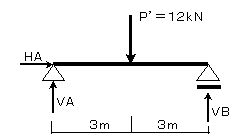
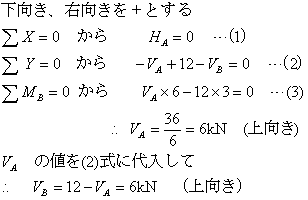
よって、答えを図に示すと以下のようになります。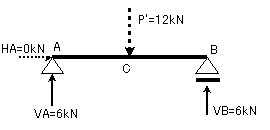
構造物を解く場合、計算式の符号が非常に重要な意味を持ちます。また、同じ符号であっても式中の符号と答えの符号とでは 意味が異なりますので混乱しないよう注意しましょう。例えば、同じマイナス(-)の符号でも、式中の(-)は力の向きを表すものであり、 計算結果の(-) というのは「仮定した力の向きと逆の向きである」という事を意味しています。
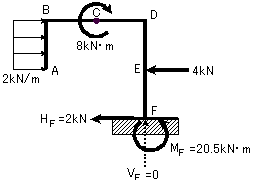
(例題2)今度は図7-3に示すラーメンの反力を求めてみましょう。 荷重がいっぱいあってややこしいかもしれませんが、落ち着いて解けば難しくはありませんよ(^ ^)
(図7-3)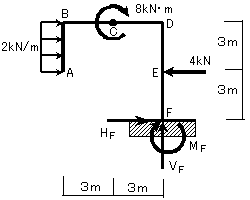

よって、図7-4に示した状態で反力を求めます。
(図7-4)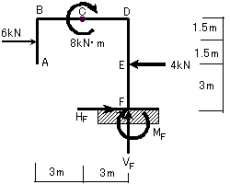
一般的に、モーメントMは力Fと距離xの積(F・x)で表され、反力算定においてもモーメントの釣合式を考える場合はF・xの式に則って計算されています。 が、部材にモーメント荷重Mxが作用している場合、これらは、すべて距離xを既に考慮したものとして荷重が与えられているので、 モーメント荷重には距離の値を乗じる必要は無いのです。よって、求める反力は図7-5のようになります。
反力の求め方は理解できましたか?反力は静定構造物を解く上で必ず必要になりますので、必ず求められるようになりましょう。
(図7-5)