構この部屋では、構造物に作用する荷重について、標記の仕方およびその値の求め方について学んでいきます。
荷重は、その作用状態から次のように分類されます。
| 荷重の種類 | 説明 | 荷重図 |
|---|---|---|
| 集中荷重 | 部材の1点に集中して作用する荷重。記号はＰ又はＷであらわす。単位にはＮ，ｋＮなどを用いる。 |  |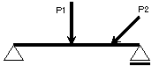
| 等分布荷重 | 部材に均等に分布して作用する荷重。記号はｗまたはＰｗであらわす。単位にはＮ／ｍ，ｋＮ／ｍ などを用いる。 |  |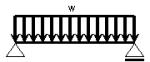
| 等変分布荷重 | 大きさが一定の割合で変化する荷重。記号はｗで表し、両端の最大値と最小値を示す。単位はＮ／ｍ，ｋＮ／ｍなどを用いる。 ※ 距離 ｘ についての一次関数として表せる。 |
 |
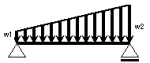| 移動荷重 | 部材に移動しながら作用する荷重。記号にはＰを用いる。単位にはＮ，ｋＮなどを用いる． |  |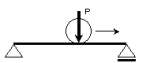
| モーメント 荷重 |
部材の1点に作用する力のモーメントの荷重。記号にはＭを用いる。単位にはＮ・ｍ，ｋＮ・ｍ などを用いる。 |  |
後から学ぶ反力の算出や静定構造物の応力を求める際、煩雑な荷重をいかにして簡単に置き換えるかということがポイントとなってきます。分布荷重が作用する場合はこれらを同じ作用をもつ集中荷重に置き換えることによって、反力の算定などが容易に行えるようになります。ここではその置き換え方について解説します。
(図１)
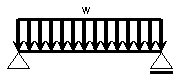
図1のように、梁に等分布荷重ｗが作用する場合について考えてみます。ただし，梁の長さ（スパン）は Ｌ とします。 分布荷重を集中荷重に置き換える場合、次の2つの決まりがあります。
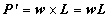
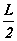の位置に生じる
図で表すと…
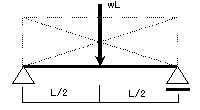
図１の梁全般にわたって等分布荷重ｗが生じている状態というのは、右の図の集中荷重ｗＬを梁の中間（Ｌ／２）の点に
載荷した場合と同じ作用があることを意味しています。
次に、図２に示すような、三角分布の等変分布荷重が作用する場合について考えてみます。
※梁の長さ（スパン）はＬとします。
三角分布の場合も、上に示した２つの決まりに従います。
よって、その大きさと作用する位置を求めると...
①荷重の大きさ＝三角形の面積なので
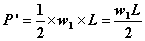
②置き換えた荷重の作用位置は三角形の重心位置なので…
梁の右側より
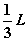の点に作用することになります。
図で表すと…
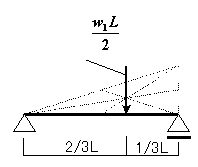
左のような状態と同じになります。
ここで学んだ、分布荷重の集中荷重への置き換え方は後で学ぶ反力などを計算する際、重要になってきますので確実にマスターしておきましょう！！
