このSTEPでは、梁、トラスと並び構造物の基本形式であり、建築の分野では最も広く用いられている 構造形式である「ラーメン」の解法について学びます。
静定梁系ラーメンは支点の他に「柱」「梁」の2つの部材で構成されています。 解法は基本的に静定梁の解き方と同じであるといえます。しかしながら、梁の場合、 水平成分の荷重が作用しない限り生じなかった軸力が、ラーメン構造の場合は水平荷重が 生じなくても部材によっては生じることがあるので注意が必要です。
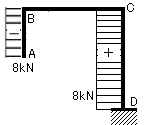
図16-1に示すような片持ち梁系ラーメンの応力を求めてみましょう。
①まず反力を求めます。
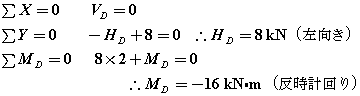
図16-2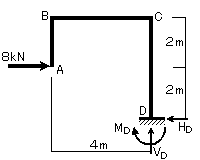
②次に図16-2に示すように部材間ごとで切断点を決めます。
基本的に1つの部材について1ヶ所の切断面を考えますが、部材の中間に集中荷重などが作用する場合は荷重に
対して部材の左右1箇所ずつ(計2箇所)を切断して考えます。(下図参照)
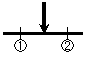
中間荷重が作用する場合はこのように切断します。
図16-2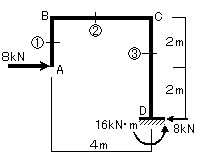
③切断点における力の釣り合いから応力を求めていきます。
①切断面(A~B間)
0≦x1≦2m
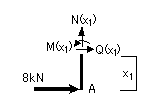
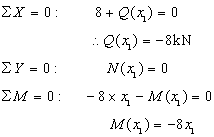
②切断面(B~C間)
0≦x2≦4m
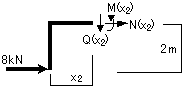
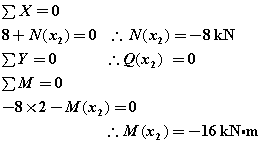
③切断面(C~D間)
0≦x3≦4m
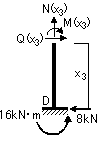
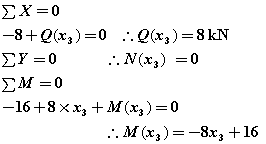
※ラーメンの場合、右柱の力のつり合いを考える時は、左側から考えると計算がややこしくなるので、 右側から解いていくと良いでしょう。(切断面の応力を仮定する場合の向きに注意しましょう。 Lesson8を参照してください)
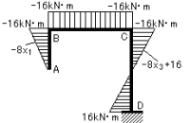
ラーメンの応力図を描く場合、下図のように内側を+、外側を-として図を描きます。
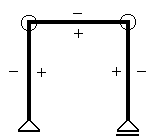
図16-1の場合で主要点の応力の値を示すと、
0≦x1≦2m x2=0:A点 x2=2:B点
N(x1)=0
Q(x1)=-8kN : Q(0)=-8kN Q(2)=-8kN
M(x1)=-8x1: M(0)=0kN・m M(2)=-16kN・m
0≦x2≦4m x2=0:B点 x2=4:C点
N(x2)=-8kN : N(0)=-8kN N(4)=-8kN
Q(x2)=0
M(x2)=-16kN : M(0)=-16kN・m M(4)=-16kN・m
0≦x3≦4m x3=0:D点 x3=4:C点
N(x3)=0
Q(x3)=8kN : Q(0)=8kN Q(4)=8kN
M(x3)=-8x3+16 : M(0)=16kN・m M(4)=-16kN・m
※ラーメンの部材の剛節点(左上の図の○部分)においては、曲げモーメントの値が一致していなければ
構造物がつり合い状態を保つことができません。よって上の場合、色付文字で示した組合せの値が等しくなければなりません。
よって各応力図を描くと…
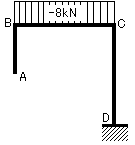 |
 |
 |
| 軸方向力図(N図) | せん断力図(Q図) | 曲げモーメント図(M図) |
次に,図16-3に示すように,支点がピンとローラーで構成された単純梁系のラーメンについて考えてみます。
①まず反力を求めます。
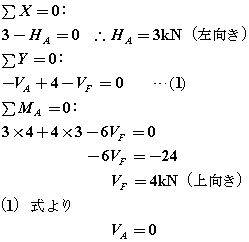
図16-3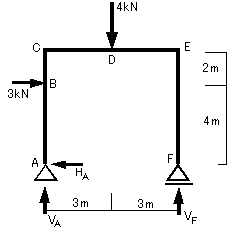
②図16-4に示すように部材の切断箇所(図中①~⑤)を決めます
図16-4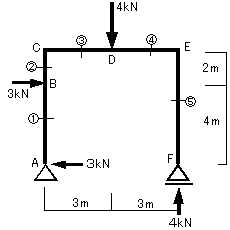
③切各切断面の力のつり合いから部材間応力を求めます。
①切断面(A~B間)
0≦x1≦4m
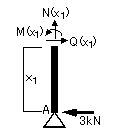
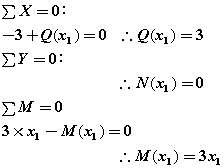
②切断面(B~C間)
0≦x2≦2m
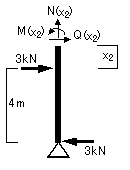
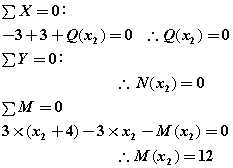
③切断面(C~D間)
0≦x3≦3m
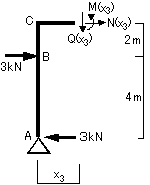
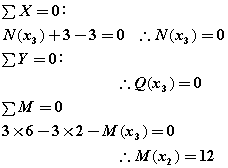
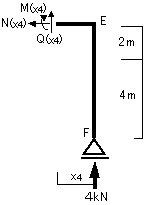
④断面:E~D間
0≦x4≦3m
④断面を考える場合、図16-3のような場合だと、構造物の右側から考えた方が、
構造物に生じる外力の数が少ないので、右側から考えます。
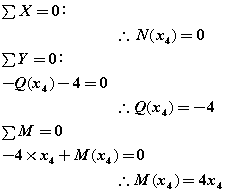
⑤断面:F~E間
0≦x5≦6m
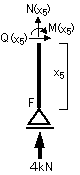
⑤断面を考える場合も同様に、右側から考えていくと、作用する外力の数が少ないため、計算が容易になります。
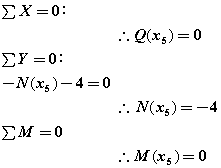
A~B間
0≦x1≦4m x1=0:A点 x1=4:B点
N(x1)=0
Q(x1)=3 : Q(0)=3kN Q(4)=3kN
M(x1)=3x1: M(0)=0kN・m M(4)=12kN・m
<B~C間>
0≦x2≦2m x2=0:B点 x2=2:C点
N(x2)=0
Q(x2)=0
M(x2)=12 : M(0)=12kN・m M(2)=12kN・m
<C~D間>
0≦x3≦3m x3=0:D点 x3=3:C点
N(x3)=0
Q(x3)=0
M(x3)=12:M(0)=12kN・m M(3)=12kN・m
<E~D間>
0≦x4≦3m x4=0:E点 x4=3:E点
N(x4)=0
Q(x4)=-4: Q(0)=-4kN Q(3)=4kN
M(x4)=4x4: M(0)=0kN・m M(3)=12kN・m
<F~E間>
0≦x5≦6m x5=0:F点 x5=6:E点
N(x5)=-4: N(0)=-4kN N(6)=-4kN
Q(x5)=0
M(x5)=0
<応力図>
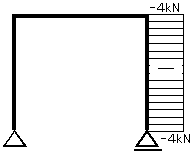
軸方向力図(N図)
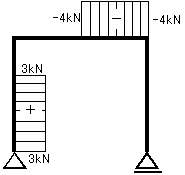
せん断力図(Q図)
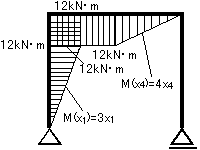
曲げモーメント図(M図)