3ヒンジ系のラーメンは両支点がピンの為、反力の未知数が4となります。したがって、 もし、部材間にヒンジがない場合は不静定構造物となり力のつり合い3条件だけでは反力を求めることができません。 しかし、部材間に1ヶ所ヒンジを設ける事でその点での曲げモーメントの値が0となります。 この条件を加える事で、3ヒンジ系ラーメンの場合、両支点がピンの場合でも、静定構造物として扱う事ができます。
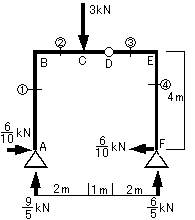
図17-1に示すような3ヒンジ系ラーメンの応力を求めましょう。
①まず反力を求めます。
右の図からもわかるように、両支点がピン支持のため、反力は4つ生じます。したがって
この場合、反力を求めるためには4つの式が必要となります。
力のつり合い式では3つまでしか反力を求めることができませんので、
支点のつり合い式だけでは反力を求める事ができません。
そこでD点がピン接合であることに注目します。
ピン接合でのモーメントの値は0となることは
Lesson12で学習しましたので、
この条件を用いるとMD=0となり、式を1つ増やす事ができます。
図17-1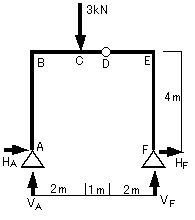
MD=0の釣り合いを考える場合は下に示すように、D点のピン接合を境にして左側部分と右側部分に
分割して、どちらかの力の釣り合いを考えればいいのです。
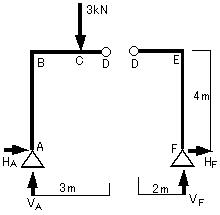
よって反力を求めると…
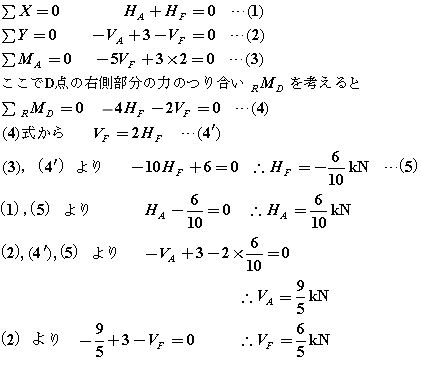
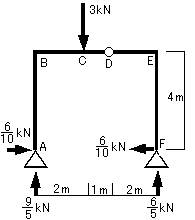
よって左の図のように反力が求められます。
あとは、これまでに学んだラーメンの解法と同様に、
部材間ごとで切断して、部材応力を求めていきます。
②ここでは下に示すように部材の切断面を設定します。
③各切断面での応力を求めます。
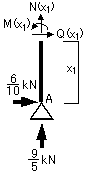
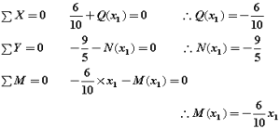
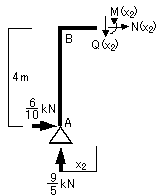
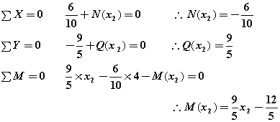
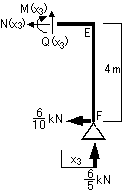
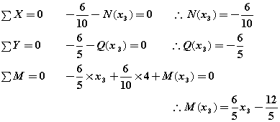
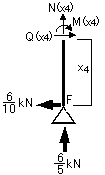
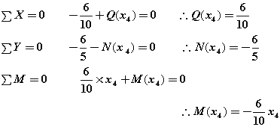
主要点での各応力度の値は・・・
よって、各応力図は…
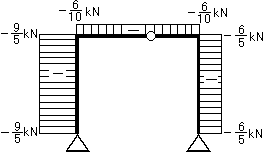 軸方向力図(N図) |
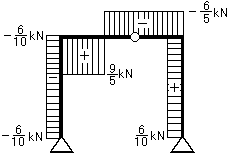 せん断力図(Q図) |
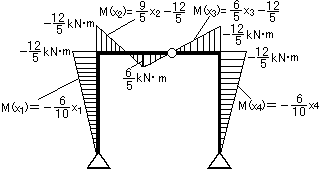
曲げモーメント図(M図) |
|