STEP1の各Lessonで構造力学を学ぶための基礎事項を学びました、それらを踏まえてここからは 実際の構造物の解き方について学んでいきます。ここからがいよいよ本題です。この部屋ではまず 構造物の基本形式である梁の解き方について学んでいく事にしましょう。
まずは梁の解き方の1つめとして、Lesson7で学んだ力の釣合条件を使って解く方法を紹介します。
※構造物を解く=応力(応力図)を求めるということです。
ここでは右の図9-1に示すような集中荷重が生じる梁を解いていきます。
(図9-1)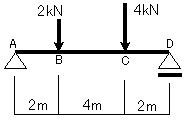
①まず、構造物に生じる反力を求めます。反力の求め方を
忘れてしまった人はLesson7をもう一度確認しましょう。
反力の仮定は図9-2に示すようになることはわかりますか?
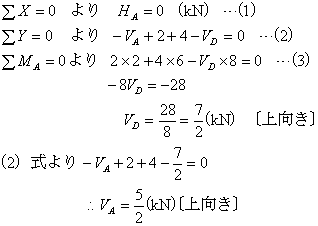
(図9-2)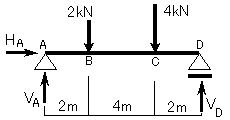
②次に図9-3に示すように支点から荷重点まで、あるいは荷重点の間での任意の点を切断して (この場合①~③点まで)、各点での力の釣合いについて考え、応力を求めていきます。
(図9-3)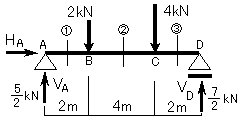
応力を仮定する場合、切断面に対して正(+)の向きになるように応力を仮定します。この場合、梁の左側から考えて いるので図のような仮定方向となります。(忘れてしまった人はLesson8を参照。図の左側だけを隠して見て下さい。 図9-4のような組合せが できると思います。)梁の右側から考える時は、 当然この場合とは逆の組合せで応力を仮定します。
(図9-4)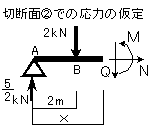
切断面①について力の釣合を考えます。
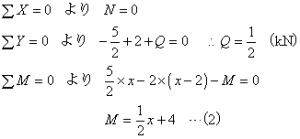
上の(1)式からも分かるように、この場合Mはスパン(x)に関する一次関数であり、荷重が作用しない
A~B間(0≦x1≦2m)までは(1)式が成り立ちます。
(図9-5)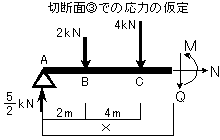
切断面②についての力の釣り合いを考えます。
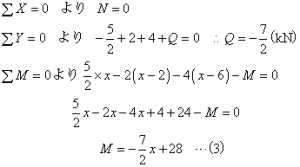
上式では切断面②についての力の釣合いを考えたので、(2)式はB~C間(2m≦x2≦6m)の範囲で成り立ちます。
さて、上のように切断面に対応する応力を求めたら、次に応力図を描きます。
応力図とはどんなものだったか忘れてしまった人は、Lesson8でもう一度確認しましょう。
まず、計算結果を整理しておくと…
ここでは、水平荷重が作用していないため軸力は生じませんので、図を描く必要はありません。
応力図では、部材軸の下側を+、上側を-とするので…
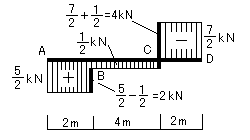
せん断力図(Q図)
左の図を見てわかるように、集中荷重の場合のせん断力図では、その値が変わる点では、 その点に作用する荷重の大きさと同じ分だけ増減する事が分かります。
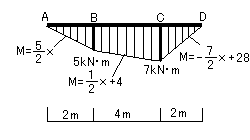
せん断力図(Q図)
この場合、荷重は集中荷重なので、モーメント図は直線になります。 よって先に求めた主要点のモーメントの値をとり、その間を結んでいけば、曲げモーメント図は描けます。