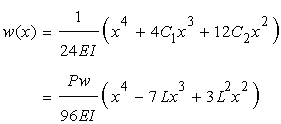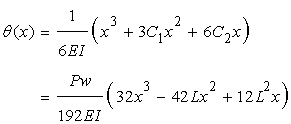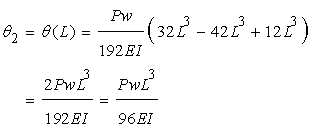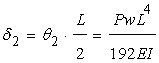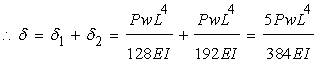ここでは様々な練習問題を解いていくことで、より理解を深めていきましょう。
右図(3-1)において、変位の最大値を求め、変形図を描きなさい。
問題を解くのに行き詰ったら、下にあるヒントをクリックし、確認しながら次に進んでいってください。
(図3-1)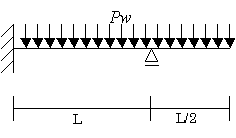
(図3-1)のような場合は次のように考えます。
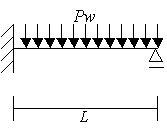
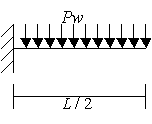
(図3-1)を上に示したように2つに分けます。次に
それぞれで求めた変位を合わせることで全体の変位を得ることができます。
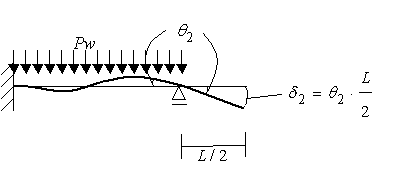
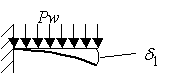
このようにして考えていってみましょう。
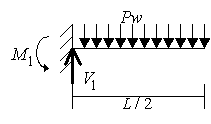
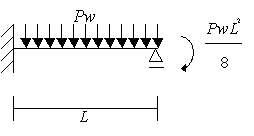
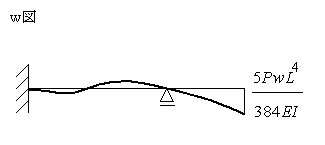
(図3-2)について考えてみます。
はじめに節点における反力と曲げモーメントを考えます。
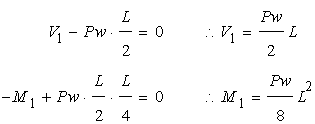
次に任意の点xにおける曲げモーメントを考えます。(図3-3)
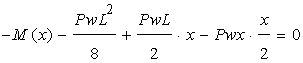
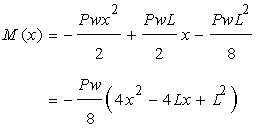
ここで梁の微分方程式より…
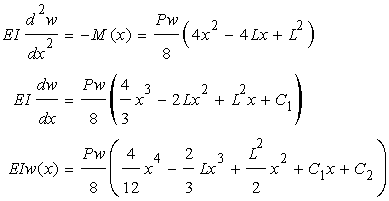
境界条件から…
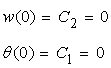
が求められるので次式が得られる
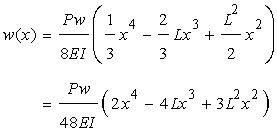
(x=L/2)のときの変位は…
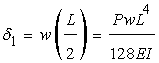
になります。
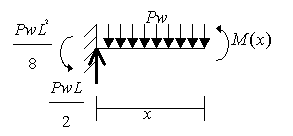
(図3-4)について考えてみます。はじめに基本式を立てます。
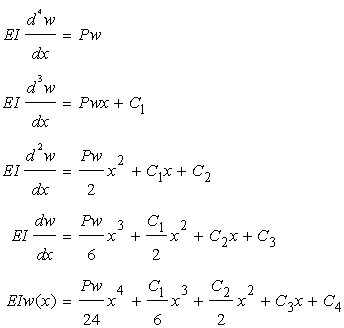
次に境界条件について考えてみます。左端は固定なので…
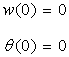
右端はローラー支持なのでM(L)=0となりますが、ここでは釣りあいを考えると…
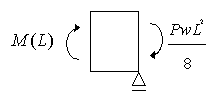
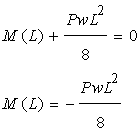
となり、境界条件は…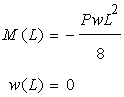
になります。
さきほど求めた境界条件から積分定数を求めます。
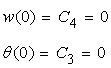
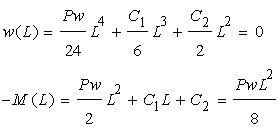
よって、次の連立方程式を解きます。
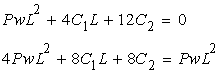
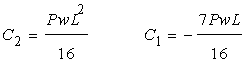
以上のように積分定数がすべて求められたので、それらを基本式に代入して変位を考えていきます。