構造物が揺れるのは、“慣性力”と“復元力”が同時に影響し合うことによるものです。
構造物自身の動きと質量による力が“慣性力”。
弾性体の変形によって、逆方向に作用する力が“復元力”です。
そして、復元力を生む弾性体の中で最も簡単なものは“ばね”なのです。
ですから構造物の揺れには、ばねが大きく関わってきます。

ちなみにここで言うばねとは、一般にイメージされるようなグルグル巻きのばねでは ありません。構造体である柱や梁を“硬いばね”に見立てて考えています。

ここでは“ばね定数”というものについて考えてみましょう。

3-1 ばね定数の求め方

ばね定数 k は次のような式で定義されています。

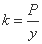
P は力の大きさ、y は変位、そしてばね定数 k は、ばねの強さ・硬さを表す量です。
各部材はばね定数 k が大きいほど「強い」とし、k が小さいほど「弱い（軟らかい）」ということになります。

このばねの式が、実際に構造物に与える影響を考えてみましょう。
さきほど考えた1層ラーメンモデルを例にとって考えてみます。変位 y は、柱と梁の曲げ剛性を EI とすると、 構造力学Ⅱで学習したたわみ角法などを用いて、

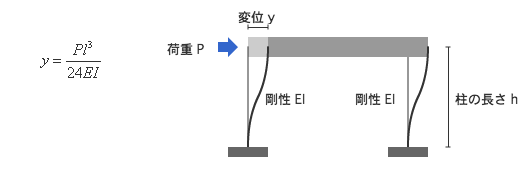
と表されるので、ばね定数 k は、

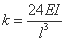
となります。
つまり、柱の長さ l が長ければ長いほど、柱のヤング係数 E や断面2次モーメント I が小さければ小さいほど、変位 y は大きくなります。 そしてそれにつれて、ばね定数 k は小さく、柔らかな構造物になっていくということが言えます。